Repasa el teorema de Pitágoras con estos recursos
Estas fichas, ejercicios online y juegos ayudarán al alumnado de Secundaria a aprender y a poner en práctica el teorema de Pitágoras.
El teorema del matemático y filósofo griego Pitágoras establece que, en todo triángulo rectángulo, la longitud de la hipotenusa es igual a la raíz cuadrada de la suma del área de las respectivas longitudes de los catetos. Una vez conocida la teoría, es el momento de practicar esta fórmula que se suele enseñar en el primer ciclo de Secundaria. Los siguientes recursos pueden ser de gran ayuda para resolver este tipo de problemas matemáticos tanto en clase como en casa.
Índice de contenidos
Juguete Montesori
Anuncio
Este tablero de madera consta de 5 piezas con las que transmitir de forma visual el teorema de Pitágoras en clase. Aunque está enfocado a niños más pequeños, es una manera ideal de crear rompecabezas para los estudiantes y, sobre todo, de enseñar la fórmula: a² + b² = c².
Puzle del teorema de Pitágoras
Anuncio
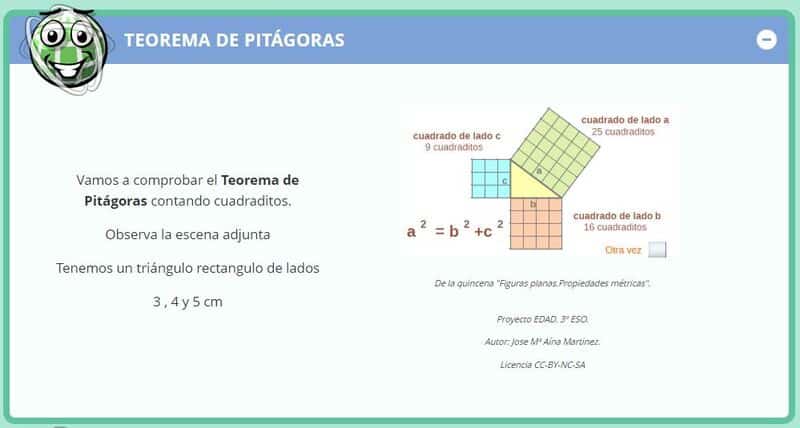
Para comprobar de manera práctica el enunciado del filósofo griego, el docente puede recurrir a una manualidad sencilla; solo necesitará cartulinas, tijeras y una regla. En esta web se encuentran las instrucciones para construir este puzle del teorema: hay que dibujar y recortar un cuadrado pequeño de 6 cm de lado, un cuadrado mediano de 8 cm de lado y un cuadrado grande de 10 cm de lado. Si el alumno consigue manipular los cuadrados pequeño y mediano de modo que cubran el grande, habrá conseguido comprobar el teorema de Pitágoras.
Juegos de educaplay
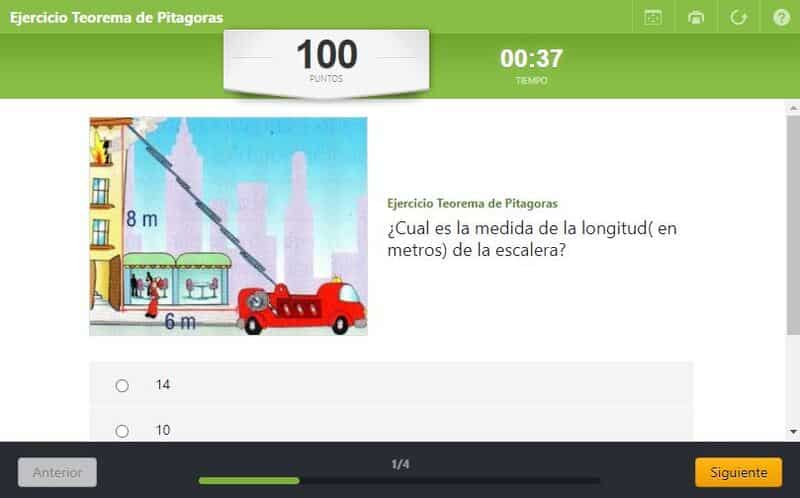
Con cuatro opciones de respuesta y a modo de test, este juego propone problemas que deben ser resueltos con la fórmula ‘a² + b² = c²’. Cada uno se ilustra con una imagen distinta y solo al final de la partida el alumno sabrá cuántos ejercicios ha resuelto correctamente. La web también dispone de un contador para ver el tiempo que tarda el estudiante en calcular lo que se pide.
Píldoras matemáticas: el teorema de Pitágoras
Después de un breve resumen con la explicación del teorema de Pitágoras, este vídeo ofrece consejos para resolver problemas matemáticos a través de la fórmula. A continuación, el autor de esta ‘píldora matemática' va presentando ejercicios de menor a mayor dificultad y resolviéndolos sobre la marcha.
Edufichas
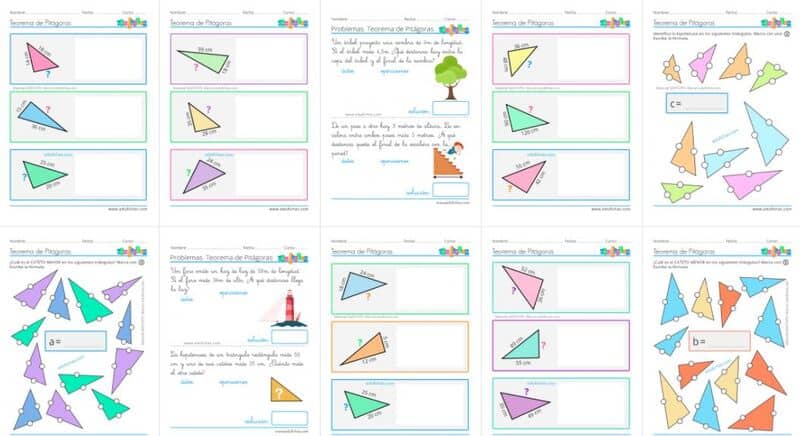
Explica de una manera sencilla qué es un triángulo rectángulo: aquel en el que uno de sus ángulos es recto, los lados que forman dicho ángulo se llaman catetos, y el lado opuesto al ángulo recto es la hipotenusa, que siempre es el lado más largo. Con esta base, enseña la fórmula del teorema de Pitágoras y propone ejercicios básicos para ponerlo en práctica. Para finalizar, recoge diez fichas imprimibles de ejercicios que ayudarán a los niños a saber identificar la hipotenusa o los catetos, a aplicar las fórmulas para hallar el valor que falta en un triángulo, y a resolver algunos problemas.
Matesfacil
Con una introducción y explicación del teorema de Pitágoras, esta página se caracteriza por presentar problemas con su solución. El estudiante se enfrenta a preguntas como la siguiente: “Si la hipotenusa de un triángulo rectángulo mide 2 cm y uno de sus lados mide 1 cm, ¿Cuánto mide el otro lado?”. Una vez respondida por el alumno, se puede desplegar una explicación completa de cómo se ha resuelto. Además, para finalizar, la web propone un test con 10 preguntas y cuatro posibles respuestas para cada una.
Material de Superprof
A modo de examen, el alumnado de los primeros cursos de ESO puede practicar lo aprendido en clase con estos cinco ejercicios. Deben rellenar la caja de respuesta y luego comprobar. Tanto si aciertan como si no, la actividad enseña los pasos a seguir para llegar a la solución correcta. Si en algún momento tienen cualquier duda, también pueden recurrir a la teoría pinchando en un enlace situado en la parte inferior.
Sobre el autor
Pepa Agüera
De pequeña preguntaba mucho y escribía otro tanto. Conjugué esas dos variables y ahora soy periodista. Me apasiona la cultura en todas sus formas, pero también la actualidad y la política. Compro libros por encima de mis posibilidades.
Muy bena la informacion