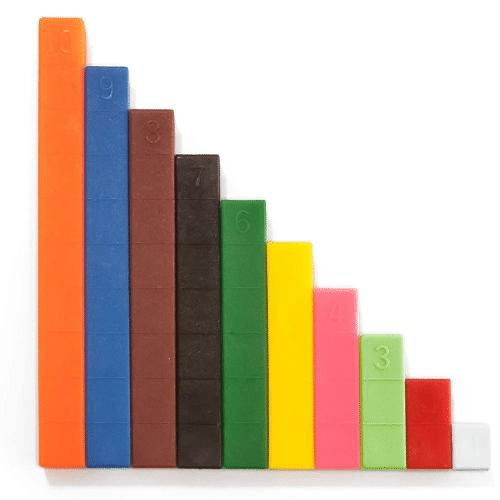
¿Conoces las Regletas de Cuisenaire? Te contamos qué son y cómo utilizarlas en el aula
Permiten sumar, restar, multiplicar y dividir de forma tangible y visual y son ideales para abordar las operaciones matemáticas en los primeros cursos de Primaria. Detallamos cómo.