Guía para aprender matemáticas con la plataforma Peyemon
Basada en el método homónimo, apuesta por centrar el aprendizaje matemático en cuestiones como los fundamentos aritméticos, algorítmicos o el diseño de rutas de aprendizaje.
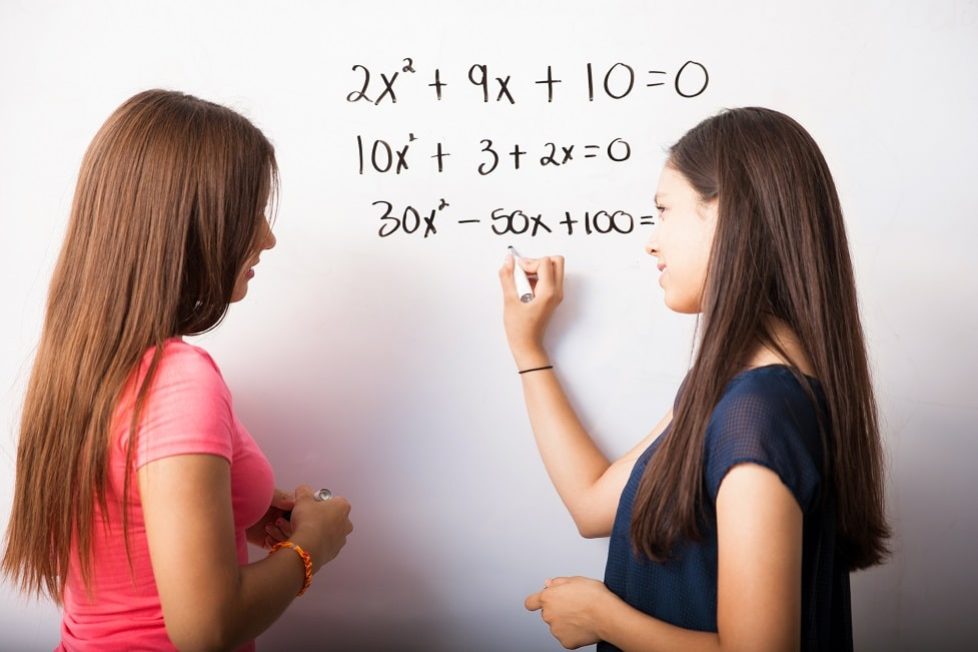
Basada en el método homónimo, apuesta por centrar el aprendizaje matemático en cuestiones como los fundamentos aritméticos, algorítmicos o el diseño de rutas de aprendizaje.
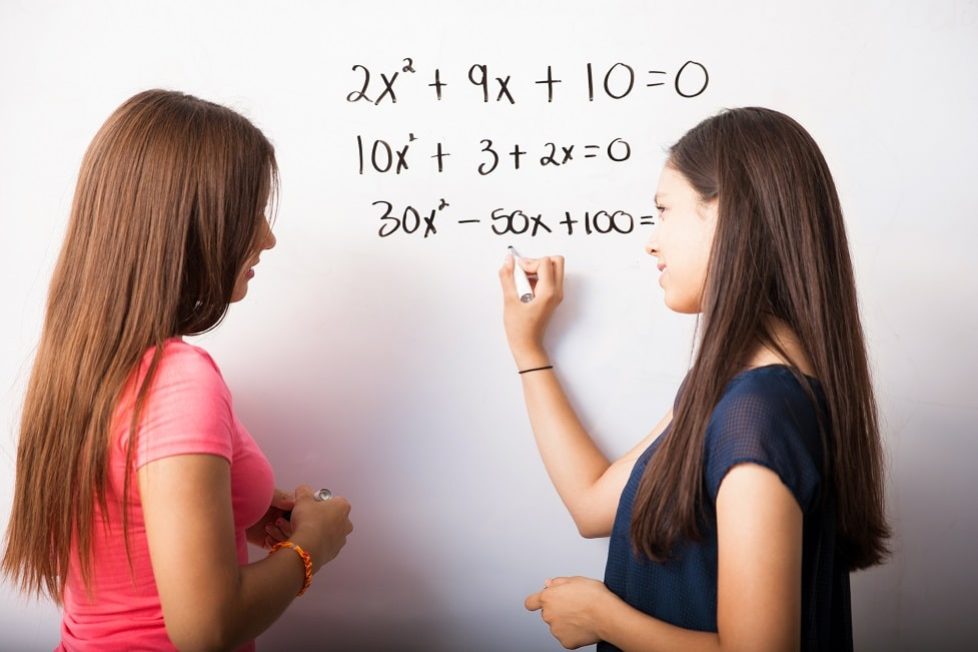
Que cualquier estudiante pueda aprender y mejorar sus habilidades en matemáticas, tanto dentro como fuera de las aulas, es el objetivo del método Peyemon; una estrategia que hace referencia al conjunto de procedimientos y contenidos digitales desarrollados por expertos en educación que ofrecen una guía sobre cómo facilitar su aprendizaje tanto a estudiantes como a docentes. Sobre este se basa la plataforma Peyemon, que precisamente busca ayudar al aprendizaje de las matemáticas apoyándose en una serie de puntos clave.
Índice de contenido:
El primero de ellos es aprender los fundamentos de la aritmética de tal forma que el alumnado domine conceptos básicos como ordenar y comparar cantidades, lectura y escritura de números, sistema de numeración decimal o tipos de números y operaciones básicas, entre otros conceptos. La importancia de aprender esto radica en que muchos temas un poco más avanzados como las sumas de fracciones, simplificación de fracciones o factores primos hacen uso de algoritmos y conceptos básicos para llegar a la solución. Al tener dominados por completo los conceptos o fundamentos, se considera cada paso del algoritmo como correcto, ya que se da por hecho que las operaciones como sumar, restar, dividir, ordenar o comparar han sido realizadas de forma correcta.
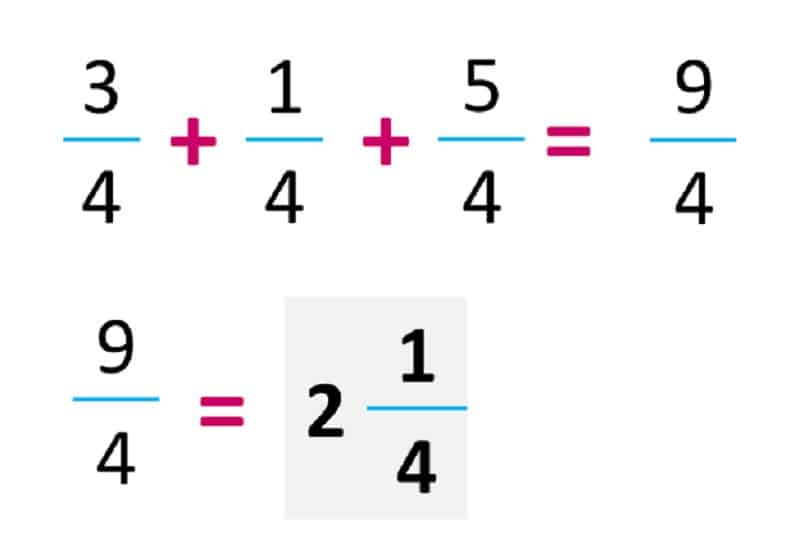
Un ejemplo para explicar este punto es la suma de fracciones homogéneas. En ella el estudiante debe conocer de forma declarativa el algoritmo más eficiente para resolver dicha operación. El primer paso es sumar todos los numeradores y escribirlos como resultado. Después, como las fracciones son homogéneas (igual denominador), el resultado parcial queda conformado por la suma de los numeradores y el denominador común. De esta manera se determina si la fracción puede simplificarse a términos más simples o valores más pequeños. Si la fracción obtenida es impropia, se procede a obtener los enteros contenidos, generando así un número mixto o simplemente un número entero según aplique.
Una vez que el estudiante conoce de forma clara el algoritmo, deberá proceder al desarrollo de la solución paso por paso, y para ello podrá hacer uso de conceptos básicos de la aritmética como:
De esta forma tanto los estudiantes como los docentes podrán identificar de manera fácil los tipos de errores cometidos, ya sean de tipo algorítmico o de concepto. Por ejemplo, se puede presentar el caso en que un estudiante conozca y desarrolle perfectamente el algoritmo pero no las operaciones fundamentales o por el contrario que no cometa ningún error al realizar las operaciones pero que el procedimiento empleado sea el incorrecto.
Ejemplo: 2 + 3 x 5 = 25
En este caso las operaciones están realizadas de forma correcta (operaciones fundamentales) pero no así el algoritmo (jerarquía de operaciones u orden de resolución), por lo que el resultado es incorrecto. Este problema suele ser muy frecuente porque el alumnado no puede identificar cuál es su error o si este está en las operaciones, conceptos o en el algoritmo empleado.
El siguiente punto clave sobre el que se apoya Peyemon tiene como objetivo que el alumnado logre aprender y desarrollar diferentes algoritmos en forma declarativa. Esto quiere decir que sean capaces de enunciar instrucciones paso por paso sin entrar en mayor detalle sobre cuál es su procedimiento interno, tal y como se vio en el ejemplo anterior de la suma de fracciones homogéneas.
Para Peyemon es fundamental que docente y estudiantes tengan a mano una ruta específica de aprendizaje para cada tema, de modo que les permita conocer cuántos conceptos en total están implicados de forma directa e indirecta. Por ejemplo, para aprender las divisiones con números naturales y decimales, el profesor deberá elaborar una ruta de aprendizaje (independientemente del nivel escolar del alumno) que le permita conocer todos los conceptos necesarios para lograr dominar la división con números naturales y decimales. Ya teniendo la ruta de aprendizaje elaborada, se puede segmentar acorde al grado escolar con el tipo (números naturales y decimales) y rango de datos (cifras de cada número).
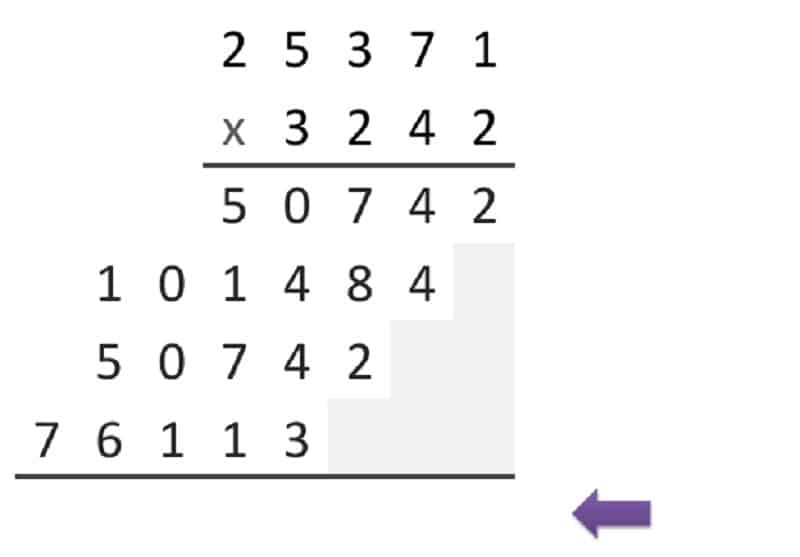
Practicar constantemente ejercicios de matemáticas mejora la lógica y análisis de los estudiantes. Sin embargo, muchos ejercicios no suelen ser fáciles de resolver dado que no está implícita la forma de proceder para su resolución. Una forma de resolver este dilema es mostrarles la lógica de desarrollo y solución de ejercicios, de tal manera que puedan por sí solos elaborar sus propios ejercicios y practicar cuantas veces sea necesario. Por ejemplo, basta con generar dos números aleatorios (naturales o decimales) para desarrollar una cantidad infinita de ejercicios de multiplicaciones con punto decimal. Una vez creado y resuelto cada ejercicio, el estudiante podrá hacer uso de la calculadora para comprobar el resultado de la multiplicación.
1 Comentarios
Excelente